C# For Dummies
Глава 7. Масиви
1. Да се напише програма, която създава масив с 20 елемента от целочислен тип и инициализира всеки от елементите със стойност равна на индекса на елемента умножен по 5. Елементите на масива да се изведат на конзолата.Упътване: Използвайте масив и
for цикъл.Решение:
Link
2. Да се напише програма, която чете два масива от конзолата и проверява дали са еднакви.
Упътване: Два масива са еднакви, когато имат еднаква дължина и стойностите на елементите в тях съответно съвпадат. Второто условие можете да проверите с
for цикъл.Решение:
Link
3. Да се напише програма, която сравнява два масива от тип char лексикографски (буква по буква) и проверява кой от двата е по-рано в лексикографската подредба.
Упътване: При лексикографската наредба символите се сравняват един по един като се започва от най-левия. При несъвпадащи символи по-рано е масивът, чийто текущ символ е по-рано в азбуката. При съвпадение се продължава със следващия символ вдясно. Ако се стигне до края на единия масив, по-краткият е лексикографски по-рано. Ако всички съответни символи от двата масива съвпаднат, то масивите са еднакви и никой о тях не е по-рано в лексикографската наредба.
Решение:
Link
4. Напишете програма, която намира максимална редица от последователни еднакви елементи в масив.
Пример: {2, 1, 1, 2, 3, 3, 2, 2, 2, 1} à {2, 2, 2}.
Упътване: Сканирайте масива отляво надясно. Всеки път, когато текущото число е различно от предходното, от него започва нова подредица, а всеки път, когато текущото число съвпада с предходното, то е продължение на текущата подредица. Следователно, ако пазите в две променливи
start и len съответно индекса на началото на текущата подредица от еднакви елементи (в началото той е 0) и дължината на текущата подредица (в началото той е 1), можете да намерите всички подредици от еднакви елементи и техните дължини. От тях лесно може да се избере най-дългата и да се запомня в две допълнителни променливи – bestStart и bestLen.Решение:
Link
5. Напишете програма, която намира максималната редица от последователни нарастващи елементи в масив.
Пример: {3, 2, 3, 4, 2, 2, 4} à {2, 3, 4}.
Упътване: Тази задача е много подобна на предходната, но при нея даден елемент се счита за продължение на текущата редица тогава и само тогава, когато е по-голям от предхождащия го елемент.
Решение:
Link
6. Напишете програма, която намира максималната подредица от нарастващи елементи в масив
arr[n]. Елементите може и да не са последователни. Пример: {9, 6, 2, 7, 4, 7, 6, 5, 8, 4} à {2, 4, 6, 8}.
Упътване: Задачата може да се реши с два вложени цикъла и допълнителен масив
len[0..n-1] . Нека в стойността len[i] пазим дължината на най-дългата нарастваща подредица, която започва някъде в масива (не е важно къде) и завършва с елемента arr[i] . Тогава len[0]=1, a len[x] е максималната сума max(1+len[prev]) , където prev < x и arr[prev] < arr[x] . Следвайки дефиницията len[0..n-1] може да се пресметне с два вложени цикъла по следния начин: първият цикъл обхожда масива последователно отляво надясно с водеща променлива x. Вторият цикъл (който е вложен в първия) обхожда масива от началото до позиция x-1 и търси елемент prev с максимална стойност на len[prev], за който arr[prev] < arr[x] . След приключване на търсенето len[x] се инициализира с 1 + най-голямата намерена стойност на len[prev] или с 1, ако такава не е намерена. Описаният алгоритъм намира дължините на всички максимални нарастващи подредици, завършващи във всеки негов елемент. Най-голямата от тези стойности е дължината на най-дългата нарастваща подредица. Ако трябва да намерим самите елементи съставящи тази максимална нарастваща подредица, можем да започнем от елемента, в който тя завършва (нека той е на индекс x), да го отпечатаме и да търсим предходния елемент (
prev). За него е в сила, че prev < x и len[x]=1+len[prev] . Така намирайки и отпечатвайки предходния елемент докато има такъв, можем да намерим елементите съставящи най-дългата нарастваща подредица в обратен ред (от последния към първия).Решение:
Link
7. Да се напише програма, която чете от конзолата две цели числа N и K (K < N), и масив от N елемента. Да се намерят тези K поредни елемента, които имат максимална сума.
Упътване: Можете да проверите коя от поредица от K числа има най-голяма сума като проверите сумите на всички такива поредици. Първата такава поредица започва от индекс 0 и завършва в индекс K-1 и нека тя има сума S. Тогава втората редица от K елемента започва от индекс 1 и завършва в индекс K, като нейната сума може да се получи като от S се извади нулевия елемент и се добави K-ти елемент. По същия начин може да се продължи до достигане на края на редицата.
Решение:
Link
8. Сортиране на масив означава да подредим елементите му в нарастващ (намаляващ) ред. Напишете програма, която сортира масив. Да се използва алгоритъма "
Selection sort".Упътване: Потърсете в Интернет информация за алгоритъма "
Selection sort" и неговите реализации. Накратко идеята е да се намери най-малкият елемент, после да се сложи на първа позиция, след това да се намери втория най-малък и да се сложи на втора позиция и т.н., докато целият масив се подреди в нарастващ ред.Решение:
Link
9. Напишете програма, която намира последователност от числа, чиито сума е максимална.
Пример: {2, 3, -6, -1, 2, -1, 6, 4, -8, 8} à 11
Упътване: Тази задача има два начина, по които може да се реши. Един от тях е с пълно изчерпване, т.е. с два цикъла проверяваме всяка възможна сума. Втория е масива да се обходи само с 1 цикъл като на всяко завъртане на цикъла проверяваме дали текущата сума е по-голяма от вече намерената максимална сума. Задачата може да се реши и с техниката "Динамично оптимиране". Потърсете повече за нея в Интернет.
Решение:
Link
10. Напишете програма, която намира най-често срещания елемент в масив.
Пример: {4, 1, 1, 4, 2, 3, 4, 4, 1, 2, 4, 9, 3} à 4 (среща се 5 пъти).
Упътване: Тази задача може да се решите по много начини. Един от тях е следният: взимате първото число и проверявате колко пъти се повтаря в масива, като пазите този брой в променлива. След всяко прочитане на еднакво число го заменяте с
int.MinValue. След това взимате следващото и отново правите същото действие. Неговия брой срещания сравнявате с числото, което сте запазили в променливата и ако то е по-голямо, го присвоявате на променливата. Както се досещате, ако намерите число равно на int.MinValue преминавате към следващото.Решение:
Link
11. Да се напише програма, която намира последователност от числа в масив, които имат сума равна на число, въведено от конзолата (ако има такава).
Пример: {4, 3, 1, 4, 2, 5, 8}, S=11 à {4, 2, 5}.
Упътване: Задачата може да се реши с два вложени цикъла. Първият задава началната позиция за втория – от първия до последния елемент. Вторият цикъл започва от позицията, зададена от първия цикъл и сумира последователно числата надясно едно по едно, докато сумата не надвиши S. Ако сумата е равна на S, се запомня числото от първия цикъл (то е началото на поредицата) и числото от втория цикъл (то е краят на поредицата).
Ако всички числа са положителни, съществува и много по-бърз алгоритъм. Сумирате числата отляво надясно като започвате от нулевото. В момента, в който текущата сума надвиши S, премахвате най-лявото число от редицата и го изваждате от текущата сума. Ако тя пак е по-голяма от търсената, премахвате и следващото число отляво и т.н. докато текущата сума не стане по-малка от S. След това продължавате с поредното число отдясно. Ако намерите търсената сума, я отпечатвате заедно с редицата, която я образува. Така само с едно сканиране на елементите на масива и добавяне на числа от дясната страна към текущата редица и премахване на числа от лявата й страна (при нужда), решавате задачата.
Решение:
Link
12. Напишете програма, която създава следните квадратни матрици и ги извежда на конзолата във форматиран вид. Размерът на матриците се въвежда от конзолата.
Пример за
(4,4):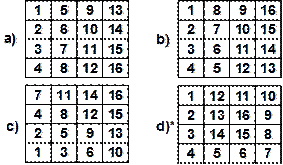
Упътване: Помислете за подходящи начини за итерация върху масивите с два вложени цикъла.
За d) може да приложите следната стратегия: започвате от позиция (0,0) и се движите надолу N пъти. След това се движите надясно N-1 пъти, след това нагоре N-1 пъти, след това наляво N-2 пъти, след това надолу N-2 пъти и т.н. При всяко преместване слагате в клетката, която напускате поредното число 1, 2, 3, ..., N.
Решение:
Link 12a
Link 12b
Link 12c
Link 12d
13. Да се напише програма, която създава правоъгълна матрица с размер n на m. Размерността и елементите на матрицата да се четат от конзолата. Да се намери подматрицата с размер
(3,3), която има максимална сума. Упътване: Погледнете предходната задача.
Решение:
Link
14. Да се напише програма, която намира най-дългата последователност от еднакви stringелементи в матрица. Последователност в матрица дефинираме като елементите са на съседни и са на същия ред, колона или диагонал.

Упътване: Задача може да се реши, като се провери за всеки елемент дали като тръгнем по диагонал, надолу или надясно, ще получим поредица. Ако получим поредица проверяваме дали тази поредица е по дълга от предходната най-дълга.
Решение:
Link
15. Да се напише програма, която създава масив с всички букви от латинската азбука. Да се даде възможност на потребител да въвежда дума от конзолата и в резултат да се извеждат индексите на буквите от думата.
Упътване: Задачата може да решите с масив и два вложени
for цикъла (по буквите на думата и по масива за всяка буква). Задачата има и хитро решение без масив: индексът на дадена главна буква ch от латинската азбука може да се сметне чрез израза: (int) ch – (int) 'A'.Решение:
Link
16. Да се реализира двоично търсене (
binary search) в сортиран целочислен масив.Упътване: Потърсете в Интернет информация за алгоритъма "
binary search". Какво трябва да е изпълнено, за да използваме този алгоритъм?.Решение:
Link
17. Напишете програма, която сортира целочислен масив по алгоритъма "
merge sort".Упътване: Потърсете в Интернет информация за алгоритъма "
merge sort" и негови реализации.Решение:
Link
18. Напишете програма, която сортира целочислен масив по алгоритъма "
quick sort".Упътване: Потърсете в Интернет информация за алгоритъма "
quick sort" и негови реализации.Решение:
Link
19. Напишете програма, която намира всички прости числа в диапазона [1…10 000 000].
Упътване: Потърсете в Интернет информация за "
Sieve of Erathostenes" (Решетото на Ератостен, учено в часовете по математика).Решение:
Link
20. Напишете програма, която по дадени N числа и число S, проверявадали може да се получи сума равна на S с използване на подмасив от N-те числа (не непременно последователни).
Пример: {2, 1, 2, 4, 3, 5, 2, 6}, S = 14 à yes (1 + 2 + 5 + 6 = 14)
Упътване: Образувайте всички възможни суми по следния алгоритъм: взимате първото число и го маркирате като "възможна сума". След това взимате следващото подред число и за всяка вече получена "възможна сума" маркирате като възможна сумата на всяка от тях с поредното число. В момента, в който получите числото
S, спирате с образуването на сумите. Можете да си пазите "възможните суми" или в булев масив където всеки индекс е някоя от сумите, или с по-сложна структура от данни (като Set например).Решение:
Link
21. Напишете програма, която по дадени
N, K и S, намира К на брой елементи измежду N-те числа, чиито сума е точно S или показва, че това е невъзможно.Упътване: Подобна на задача 20 с тази разлика, че ако сумата е равна на
S, но броя елементи е различен от К, продължаваме да търсим. Помислете как да пазите броя числа, с които сте получили определена сума.Решение:
Link
22. Напишете програма, която прочита от конзолата масив от цели числа и премахва минимален на брой числа, така че останали числа да са сортирани в нарастващ ред. Отпечатайте резултата.
Пример: {6, 1, 4, 3, 0, 3, 6, 4, 5} à {1, 3, 3, 4, 5}
Упътване: Задачата може да се реши като се направи допълнителен масив със дължина броя на елементите. В този масив ще пазим текущата най-дълга редица с край елемента на този индекс.
Решение:
Link
23. Напишете програма, която прочита цяло число N от конзолата и отпечатва всички пермутации на числата [1…N].
Пример: N = 3 à {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}
Упътване: Задачата може да се реши с рекурсия. Напишете подходяща рекурсия и всеки път променяме позицията на всеки елемент.
Решение:
Link
← Обратно