C# For Dummies
Глава 10. Рекурсия
1. Напишете програма, която симулира изпълнението на n вложени цикъла от 1 до nУпътване: Направете метод, в който има цикъл и за всяко завъртане на цикъла да се вика същия метод.
Решение:
Link
2. Напишете рекурсивна програма, която генерира и отпечатва всички комбинации с повторение на k елемента над n-елементно множество.
Примерен вход:
n = 3, k = 2Примерен изход:
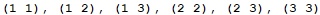
Измислете и реализирайте итеративен алгоритъм за същата задача.
Упътване: И за рекурсивния и за итеративния вариант на задачата използвайте модификация на алгоритмите за генериране на N вложени цикли.
Решение:
Link
3. Напишете рекурсивна програма, която генерира всички вариации с повторение на n елемента от k-ти клас.
Примерен вход:
n = 3, k = 2Примерен изход:
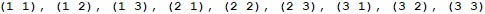
Измислете и реализирайте итеративен алгоритъм за същата задача.
Упътване: И за рекурсивния и за итеративния вариант на задачата използвайте модификация на алгоритмите за генериране на N вложени цикли.
Решение:
Link
4. Нека е дадено множество от символни низове. Да се напише рекурсивна програма, която генерира всички подмножества съставени от точно k на брой символни низа, избрани измежду елементите на това множество.
Примерен вход:

Примерен изход:
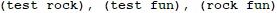
Упътване: Нека низовете са N на брой. Използвайте имитация на k вложени цикли (рекурсивна или итеративна). Трябва да генерирате всички множества от k елемента в диапазона
[0...N-1] . За всяко такова множество разглеждате числата от него като индекси в масива със символните низове и отпечатвате за всяко число съответния низ. За горния пример множеството {0, 2} означава нулевата и втората дума, т.е. (test, fun).Решение:
Link
5. Напишете рекурсивна програма, която отпечатва всички подмножества на дадено множество от думи.
Примерен вход:
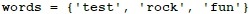
Примерен изход:
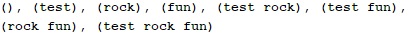
Измислете и реализирайте итеративен алгоритъм за същата задача.
Упътване: Можете да използвате предходната задача и да я извикатe
N пъти, за да генерирате последователно празното множество (k=0) , следвано от всички подмножества с 1 елемент (k=1) , всички подмножества с 2 елемента (k=2) , всички подмножества с 3 елемента (k=3) и т.н.Решение:
Link
6. Реализирайте алгоритъма \"сортиране чрез сливане\" (merge-sort). При него началният масив се разделя на две равни по големина части, които се сортират (рекурсивно чрез merge-sort) и след това двете сортирани части се сливат, за да се получи целият масив в сортиран вид.
Упътване: Ако се затрудните, потърсете \"merge sort\" в Интернет. Ще намерите стотици имплементации, включително на C#. Предизвикателството е да не се заделя при всяко рекурсивно извикване нов масив за резултата, защото това е неефективно, а да се ползват само 3 масива в цялата програма: двата масива, които се сливат и трети за резултата от сливането. Ще трябва да реализирате сливане две области от масив в област от друг масив.
Решение:
Link
7. Напишете рекурсивна програма, която генерира и отпечатва пермутациите на числата 1, 2, …, n, за дадено цяло число n.
Примерен вход:
n = 3Примерен изход:
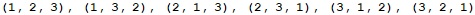
Упътване: Да предположим, че методът
Perm(k) пермутира по всички възможни начини елементите от масив p[], стоящи на позиции от 0 до k включително. В масива p първоначално записваме числата от 1 до N.Можем да реализираме рекурсивно
Perm(k) по следния начин: При k=0 отпечатваме поредната пермутация и излизаме (дъно на рекурсията).
За всяка позиция i от 0 до k-1 извършваме следното:
a. Разменяме
p[i] с p[k].b. Извикваме рекурсия:
Perm(k-1).c. Разменяме обратно
p[i] с p[k].Извикваме
Perm(k-1).В началото започваме с извикване на
Perm(N-1).Решение:
Link
8. Даден е масив с цели числа и число N. Напишете рекурсивна програма, която намира всички подмножества от числа от масива, които имат сума N. Например ако имаме масива
{2, 3, 1, -1} и N=4, можем да получим N=4 като сума по следните два начина: 4=2+3-1; 4=3+1.Упътване: Задачата не се различава съществено от задачата за намиране на всички подмножества измежду даден списък със символни низове. Помислете ще работи ли бързо програмата при 500 числа? Обърнете внимание, че трябва да отпечатаме всички подмножества със сума N, които могат да бъдат ужасно много при голямо N и подходящи числа в масива. По тази причина задачата няма ефективно решение.
Решение:
Link
9. Даден е масив с цели положителни числа. Напишете програма, която проверява дали в масива съществуват едно или повече числа, чиято сума е N. Можете ли да решите задачата без рекурсия?
Упътване: Ако подходите към проблема по метода на изчерпването на всички възможности, решението няма да работи при повече от 20-30 еле¬мента. Затова може да подходите по съвсем различен начин в случай, че числата в масива са само положителни или са ограничени в някакъв диапазон (примерно
[-50…50] ). Тогава може да се използва следният оптимиза¬ционен алгоритъм с динамично оптимиране: Нека имаме масива с числа
p[]. Нека означим с possible(k, sum) дали можем да получим сума sum като използваме само числата p[0], p[1], ..., p[k] . Тогава са в сила следните рекурентни зависимости: -
possible(0, sum) = true, точно когато p[0] == sum-
possible(k, sum) = true, точно когато possible[k-1, sum] == true или possible[k-1, sum-p[k]] == trueГорната формула показва, че можем да получим сума
sum от елемен¬тите на масива на позиции от 0 до k, ако едно от двете е в сила: - Елементът
p[k] не участва в сумата sum и тя се получава по някакъв начин от останалите елементи (от 0 до k-1); - Елементът
p[k] участва в сумата sum, а остатъкът sum-p[k] се получава по някакъв начин от останалите елементи (от 0 до k-1).Реализацията не е сложна, но трябва да внимавате и да не позволя¬вате вече сметната стойност от двумерния масив
possible[,] да се пресмята повторно. За целта трябва да пазите за всяко възможно k и sum стойността possible[k, sum] . Иначе алгоритъмът няма да работи при повече 20-30 елемента. Възстановяването на самите числа, които съставят намерената сума, може да се извърши като се тръгне отзад напред от сумата n, получена от първите
k числа, като на всяка стъпка се търси как тази сума може да се получи чрез първите k-1 числа (чрез взимане на k-тото число или пропускането му). Имайте предвид, че в общия случай всички възможни суми на числа от входния масив може да са ужасно много. Примерно всички възможни суми от 50
int числа в интервала [Int32.MinValue… Int32.MaxValue] са достатъчно много, че да не могат да се съберат в каквато и да е структура от данни. Ако обаче всички числа във входния масив са положителни (както е в нашата задача), може да пазите само сумите в интервала [1..N], защото от останалите са безперспективни и от тях не може да се получи търсената сума N чрез добавяне на едно или повече числа от входния масив. Ако числата във входния масив не са задължително положителни, но са ограничени в някакъв интервал, тогава и всички възможни суми са ограничени в някакъв интервал и можем да ползваме описания по-горе алгоритъм. Например, ако диапазонът на числата във входния масив е от -50 до 50, то най-малката възможна сума е
-50*N, а най-голямата е 50*N. Ако числата във входния масив са произволни и не са ограничени в някакъв интервал, задачата няма ефективно решение.
Можете да прочетете повече за тази класическа оптимизационна задача в Уикипедия:
http://en.wikipedia.org/wiki/Subset_sum_problem .
Решение:
Link
10. Дадена е матрица с проходими и непроходими клетки. Напишете рекурсивна програма, която намира всички пътища между две клетки в матрицата.
Упътване: Прочетете за All Depth-First Search в интернет.
Решение:
Link
← Обратно