C# For Dummies
Chapter 6. Loops
1. Write a program that prints on the console the numbers from 1 to N. The number N should be read from the standard input.Guidelines: Use a
for-loop.Solution:
static void Main(string[] args)
{
Console.Write("Enter first number: ");
int length = Int32.Parse(Console.ReadLine());
for (int i = 1; i < length; i++)
Console.WriteLine(i);
}
{
Console.Write("Enter first number: ");
int length = Int32.Parse(Console.ReadLine());
for (int i = 1; i < length; i++)
Console.WriteLine(i);
}
2. Write a program that prints on the console the numbers from 1 to N, which are not divisible by 3 and 7 simultaneously. The number N should be read from the standard input.
Guidelines: Use a
for-loop and the operator % for finding the remainder in integer division. A number number is not divisible by 3 and 7 simultaneously exactly when (num % (3*7) == 0).Solution:
Link
3. Write a program that reads from the console a series of integers and prints the smallest and largest of them.
Guidelines: First read the count of numbers, for example in a variable
n. Then consequently enter n numbers with one for loop. While entering each new number, save in two variables the smallest and the largest number until this moment. At the start initialize the smallest and the largest number with Int32.MaxValue and Int32.MinValue respectively.Solution:
Link
4. Write a program that prints all possible cards from a standard deck of cards, without jokers (there are 52 cards: 4 suits of 13 cards).
Guidelines: Number the cards from 2 to 14 (these numbers will match the cards 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A). Number the suits from 1 to 4 (1 – club, 2 – diamond, 3 – heart and 4 – spades). Now you can use the two nested loops and print each of the cards with two
switch statements.Solution:
Link
5. Write a program that reads from the console number N and print the sum of the first N members of the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
Guidelines: Fibonacci numbers start from 0 and 1, each additional is obtained as the sum of the previous two. You can find the first
n Fibonacci numbers with a for-loop from 1 to n, and at each iteration calculate the next number by using the previous two (which you will keep in two additional variables).Solution:
Link
6. Write a program that calculates N!/K! for given N and K (1 < K < N).
Guidelines: Multiply the numbers from K+1 to N (think why this is correct).
Solution:
static void Main(string[] args)
{
Console.Write("Enter N: (1<K<N) ");
int n = Int32.Parse(Console.ReadLine());
Console.Write("Enter K: (1<K<N) ");
int k = Int32.Parse(Console.ReadLine());
for (int i = n - 1; i > 0; i--)
{
n *= i;
}
for (int i = k - 1; i > 0; i--)
{
k *= i;
}
n /= k;
Console.WriteLine("Result is {0}", n);
}
{
Console.Write("Enter N: (1<K<N) ");
int n = Int32.Parse(Console.ReadLine());
Console.Write("Enter K: (1<K<N) ");
int k = Int32.Parse(Console.ReadLine());
for (int i = n - 1; i > 0; i--)
{
n *= i;
}
for (int i = k - 1; i > 0; i--)
{
k *= i;
}
n /= k;
Console.WriteLine("Result is {0}", n);
}
7. Write a program that calculates N!*K!/(N-K)! for given N and K (1 < K < N).
Guidelines: One solution is to calculate separately each factorial and at the end to perform the respective operations with the results.
Think how you can optimize the calculations, in order to not calculate too many factorials! In fractions of factorials there are many possibilities to reduce the same factors in the numerator and denominator. These optimizations will not only reduce the calculations and increase the performance but will save you from overflows in some situations. You might need to use arrays
num[0..N] and denum[0..n] to hold the factors in the numerator and in the denominator and to cancel the fraction.Solution:
Link
8. In combinatorics, the Catalan numbers are calculated by the following formula:
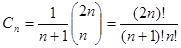, for n ≥ 0.Write a program that calculates the n-th Catalan number by given n.
Guidelines: Use the same concept of canceling the faction of simple factors, like you probably did in the previous problem.
Solution:
Link
9. Write a program that for a given integers n and x, calculates the sum:
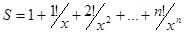
Guidelines: You can solve the problem with a
for-loop for k=0…n, by using three additional variables factorial, power and sum in which you will keep for the k-th iteration of the loop respectively k!, x-k and the sum of the first k members of sequence. If your implementation is good, you should have only one loop and you should not use external functions to calculate factorials and to raise power.Solution:
static void Main(string[] args)
{
int sum = 1, temp = 1;
Console.Write("Enter n: ");
int n = Int32.Parse(Console.ReadLine());
Console.Write("Enter x: ");
int x = Int32.Parse(Console.ReadLine());
for (int i = 1; i <= n; i++)
{
temp *= i / x;
sum += temp;
}
Console.WriteLine("Result is {0}", sum);
}
{
int sum = 1, temp = 1;
Console.Write("Enter n: ");
int n = Int32.Parse(Console.ReadLine());
Console.Write("Enter x: ");
int x = Int32.Parse(Console.ReadLine());
for (int i = 1; i <= n; i++)
{
temp *= i / x;
sum += temp;
}
Console.WriteLine("Result is {0}", sum);
}
10. Write a program that reads from the console a positive integer number N (N < 20) and prints a matrix of numbers as on the figures below:
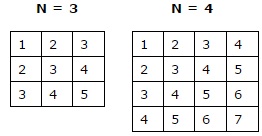
Guidelines: You should use two nested loops, similar to the problem \"Printing a Triangle\". The outer loop must run from 1 to N, and the inner – from the value of the outer loop to the value of the outer loop + N - 1.
Solution:
static void Main(string[] args)
{
Console.Write("Enter N: (N < 20) ");
int n = Int32.Parse(Console.ReadLine());
for (int i = 1; i <= n; i++)
{
for (int j = i; j <= i; j++)
{
Console.Write("{0} ", j);
}
Console.WriteLine();
}
}
{
Console.Write("Enter N: (N < 20) ");
int n = Int32.Parse(Console.ReadLine());
for (int i = 1; i <= n; i++)
{
for (int j = i; j <= i; j++)
{
Console.Write("{0} ", j);
}
Console.WriteLine();
}
}
11. Write a program that calculates with how many zeroes the factorial of a given number ends. Examples:
N = 10 -> N! = 3628800 -> 2
N = 20 -> N! = 2432902008176640000 -> 4
Guidelines: The number of zeros at the end of n! depends on how many times the number 10 is a divisor of the factorial. Because the product 1*2*3…*n has a greater number of divisors 2, than 5 and because 10 = 2 * 5, then the number of zeros in n! is exactly as many as the multipliers with value 5 in the product 1 * 2 * 3 * … * n. Because every fifth number is divisible by 5, and every 25th number is divisible by 5 two times, etc., the number of zeros in n! is the sum: n/5 + n/25 + n/125 + …
Solution:
static void Main(string[] args)
{
Console.Write("Enter N: ");
decimal n = Int32.Parse(Console.ReadLine());
int zeroes = 0;
for (int i = (int)(n - 1); i > 0; i--)
n *= i;
Console.Write("N! is {0} and it ends ", n);
do
{
n /= 10;
zeroes++;
} while (n % 10 == 0);
Console.WriteLine("with {0} zeroes.", zeroes);
}
{
Console.Write("Enter N: ");
decimal n = Int32.Parse(Console.ReadLine());
int zeroes = 0;
for (int i = (int)(n - 1); i > 0; i--)
n *= i;
Console.Write("N! is {0} and it ends ", n);
do
{
n /= 10;
zeroes++;
} while (n % 10 == 0);
Console.WriteLine("with {0} zeroes.", zeroes);
}
12. Write a program that converts a given number from decimal to binary notation (numeral system).
Guidelines: Read in Wikipedia what numeral systems are.
Solution:
static void Main(string[] args)
{
Console.Write("Enter number: ");
int n = Int32.Parse(Console.ReadLine());
string binary = Convert.ToString(n, 2);
Console.WriteLine("Result is {0}", binary);
}
{
Console.Write("Enter number: ");
int n = Int32.Parse(Console.ReadLine());
string binary = Convert.ToString(n, 2);
Console.WriteLine("Result is {0}", binary);
}
13. Write a program that converts a given number from binary to decimal notation.
Guidelines: See the previous problem.
Solution:
static void Main(string[] args)
{
Console.Write("Enter binary number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 2), 10);
Console.WriteLine("Result is {0}", toDecimal);
}
{
Console.Write("Enter binary number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 2), 10);
Console.WriteLine("Result is {0}", toDecimal);
}
14. Write a program that converts a given number from decimal to hexadecimal notation.
Guidelines: See the previous problem.
Solution:
static void Main(string[] args)
{
Console.Write("Enter decimal number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 10), 16);
Console.WriteLine("Result is {0}", toDecimal);
}
{
Console.Write("Enter decimal number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 10), 16);
Console.WriteLine("Result is {0}", toDecimal);
}
15. Write a program that converts a given number from hexadecimal to decimal notation.
Guidelines: See the previous problem.
Solution:
static void Main(string[] args)
{
Console.Write("Enter decimal number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 16), 10);
Console.WriteLine("Result is {0}", toDecimal);
}
{
Console.Write("Enter decimal number: ");
int n = Int32.Parse(Console.ReadLine());
string toDecimal = Convert.ToString(Convert.ToInt32(n, 16), 10);
Console.WriteLine("Result is {0}", toDecimal);
}
16. Write a program that by a given integer N prints the numbers from 1 to N in random order.
Guidelines: Search in the Internet for information about the class
System.Random. Read in the Internet about arrays. Create an array with N elements and write in it the numbers from 1 to N. After that a few times (think exactly how many) swap two random pairs of elements from the array.string.Solution:
Link
17. Write a program that given two numbers finds their greatest common divisor (GCD).
Guidelines: Search the Internet for the Euclidean algorithm for calculation the greatest common divisor (CGD) or read about it in Wikipedia.
Solution:
static void Main(string[] args)
{
Console.Write("Enter first number: ");
int a = Int32.Parse(Console.ReadLine());
Console.Write("Enter second number: ");
int b = Int32.Parse(Console.ReadLine());
while (a != 0 && b != 0)
{
if (a > b) a %= b;
else b %= a;
}
if (a == 0) Console.WriteLine(b);
else Console.WriteLine(a);
}
{
Console.Write("Enter first number: ");
int a = Int32.Parse(Console.ReadLine());
Console.Write("Enter second number: ");
int b = Int32.Parse(Console.ReadLine());
while (a != 0 && b != 0)
{
if (a > b) a %= b;
else b %= a;
}
if (a == 0) Console.WriteLine(b);
else Console.WriteLine(a);
}
18. Write a program that for a given number n, outputs a matrix in the form of a spiral: Example with n=4:
| 1 | 2 | 3 | 4 |
| 12 | 13 | 14 | 5 |
| 11 | 16 | 15 | 6 |
| 10 | 9 | 8 | 7 |
Guidelines: You should use a two-dimensional array (matrix). The algorithm of filling a spiral matrix in not straightforward and may require a bit of thinking.
Solution:
Link
← Back