C# For Dummies
Chapter 10. Recursion
1. Write a program to simulate n nested loops from 1 to n.Guidelines: Create a recursive method Loops(int k), perform a for-loop from 1 to n and make a recursive call Loops(k-1) in the loop. The bottom of the recursion is when k < 0. Initially invoke Loops(n-1).
Solution:
Link
2. Write a program to generate all variations with duplicates of
n elements class k.Example input:
n = 3, k = 2Example output:
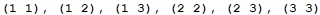
Think about and implement an iterative algorithm as well.
Guidelines: The recursive solution is to modify the algorithm for generating N nested loops. In fact you need k nested loops from 1 to n.
The iterative solution is as follows: start from the first variation in the lexicographical order: {1, 1, …, 1} k times. To obtain the next variation, increase the last number. If it becomes greater than n, change it to 1 and increase the next number on the left. Do the same on the left until the first number goes greater than n.
Solution:
Link
3. Write a program to generate and print all combinations with duplicates of
k elements from a set with n elements.Example input: br />
n = 3, k = 2Example output:
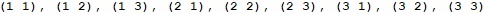
Think about and implement an iterative algorithm as well.
Guidelines: Modify the algorithms from the previous problem and always keep each number equal or greater than the number on the left of it. The easiest way to achieve this is to generate k nested loops from 1 to n and print only these combinations in which each number is greater or equal than the number on its left. You may optimize this approach to get generate directly an increasing sequence for better performance.
Solution:
Link
4. You are given a set of strings. Write a recursive program, which generates all subsets, consisting exactly
k strings chosen among the elements of this set.Example input:

Example output:
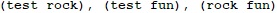
Guidelines: Let the strings’ count be
n. Use the implementation of k nested loops (recursive or iterative) with additional limitation that each number is greater than the previous one. Thus you will generate all different subsets of k elements in the range [0…n-1]. For each set consider the numbers from it as indices in the array of strings and print for each number the corresponding string. For the example above, the set {0, 2} corresponds to the strings at position 0 and position 2, i.e. (test, fun).The iterative algorithm is similar to the iterative algorithm for generating n nested loops, but is more complicated because it needs to guarantee that each number is greater than the number on its left.
Solution:
Link
5. Write a recursive program, which prints all subsets of a given set of N words.
Example input:
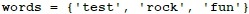
Example output:
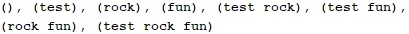
Think about and implement an iterative algorithm as well.
Guidelines: You can use the previous task and call it N times in order to generate consequently the empty set
(k=0) , followed by the all subsets with one element (k=1) , all subsets with 2 elements (k=2), all subsets with 3 elements (k=3), etc. The problem has another very smart iterative solution: run a loop from 0 to 2N-1 and convert each of these numbers to binary numeral system. For example, for
N=3 you will have the following binary representations of the numbers between 0 to 2N-1: 000, 001, 010, 011, 100, 101, 110, 111Now for each binary representation take those words from the subset for which have bit 1 on the corresponding position in the binary representation. For instance, for the binary representation \"101\" take the first and the last string (at these positions there is 1) and omit the second string (at this position there is 0). Smart, isn’t it?
Solution:
Link
6. Implement the merge-sort algorithm recursively. In it the initial array is divided into two equal in size parts, which are sorted (recursively via merge-sort) and after that the two sorted parts are merged in order to get the whole sorted array.
Guidelines: In case you have any difficulties search in Internet for \"merge sort\". You are going to find hundreds of implementations, including in C#. The challenge is to avoid allocating a new array for the result at each recursive call, because this is inefficient, and to use only three arrays in the whole program: two arrays to be merged merge and a third for the result from the merging. You will have to implement merging of two ranges of an array into a range of another array.
Solution:
Link
7. Write a recursive program, which generates and prints all permutations of the numbers
1, 2, …, n, for a given integer n.Example input:
n = 3Example output:
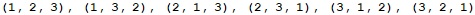
Guidelines: Recursive algorithm: suppose that the method
Perm(k) permutes in all possible ways the elements of the array p[] at positions from 0 to k-1 (inclusive). Firstly, initialize the array p with the numbers from 1 to N. Implement recursively Perm(k) in the following way:1. If
k==0, print the current permutation and exit the recursion (bottom of the recursion).2. Call
Perm(k-1).3. For each position
i from 0 to k-1 do the following:a. Swap
p[i] with p[k].b. Recursively call
Perm(k-1).c. Swap back
p[i] with p[k].In the beginning call
Perm(k-1) to start the recursive generation.Iterative algorithm: Read in Wikipedia how to generate from given permutation the next permutation in the lexicographic order iteratively: en.wikipedia.org/wiki/Permutation#Generation_in_lexicographic_order.
Solution:
Link
8. You are given an array of integers and a number
N. Write a recursive program that finds all subsets of numbers in the array, which have a sum N. For example, if we have the array {2, 3, 1, -1} and N=4, we can obtain N=4 as a sum in the following two ways: 4=2+3-1; 4=3+1.Guidelines: The problem is not very different from the task with finding all subsets among a given list of strings. Shall it work fast enough with 500 numbers? Pay attention that we have to print all subsets with sum N which can be really big amount if
N is very big and proper numbers exist in the array. For this reason the task has no efficient solutionSolution:
Link
9. . You are given an array of positive integers. Write a program that checks whether there is one or more numbers in the array (subset), whose sum is equal to S. Can you solve the task efficiently for large arrays?
Guidelines: If we approach the problem by the method of generating of all possibilities, the solution will not work for more than 20-30 numbers. That’s why we may approach it in a very different way in case the elements of the array are only positive, or are limited in a certain range (for example
[-50…50]). Then we could use the following optimized algorithm based on dynamic programming:Assume we are given an array of numbers
p[]. Let’s denote by possible(k, sum) whether we could obtain sum by using only the numbers first k numbers (p[0], p[1], …, p[k]). Then, the following recurrent dependencies are valid: -
possible(0, sum) = true if p[0] == sum-
possible(k, sum) = true if possible[k-1, sum] == true or possible[k-1, sum-p[k]] == trueThe formula above shows that we can obtain
sum from the elements of the array at positions 0 to k if one of the following two statements remains: - The element
p[k] does not participate in the sum and the sum is obtained from the rest of the elements (from 0 to k-1);- The element
p[k] participates in sum and the remainder sum-p[k] is obtained from the rest of the elements (from 0 to k-1).The implementation is not complex. Just calculate the recursive formulas by recursive method. We should be careful and not let already calculated values from the two-dimensional array
possible[,] to be calculated twice. For this purpose we should keep for each possible k and sum the value possible[k,sum]. Otherwise the algorithm will not work for more than 20-30 elements. The regeneration of the numbers, which compose the found sum, may be implemented if we go backwards from the sum n, obtained from the first
k numbers. At each step we examine how this sum can be obtained from the first k–1 numbers (by taking the kth number or omitting it). Bear in mind that in the general case all possible sums of the numbers from the input array may be an awful lot. For instance, possible sums of 50
int numbers in the range [Int32.MinValue …Int32.MaxValue] are enough so that we could not sum them in whatever data structure. If, however, all numbers in the input array are positive (as in our case), we could keep the sums in the range [1…S] because from the rest we could not obtain sum S by adding one or more numbers from the input array. If the numbers in the input array are not mandatory positive, but are limited in a range, then all possible sums are limited in some range too and we could use the algorithm described above. For example, if the range of numbers is from -50 to 50, then the least sum is -50*S and the greatest is 50*S.
If the numbers in the input array are random and not limited in a range, then the problem has no efficient solution.
You could read more about this classical optimization problem in computer science called “Subset Sum Problem” in the following article in Wikipedia: http://en.wikipedia.org/wiki/Subset_sum_problem .
Solution:
Link
10. You are given a matrix with passable and impassable cells. Write a recursive program that finds all paths between two cells in the matrix.
Guidelines: Note that you need to find all possible paths (not just one of them) so don’t expect your program to run fast for large input data.
Solution:
Link
← Back